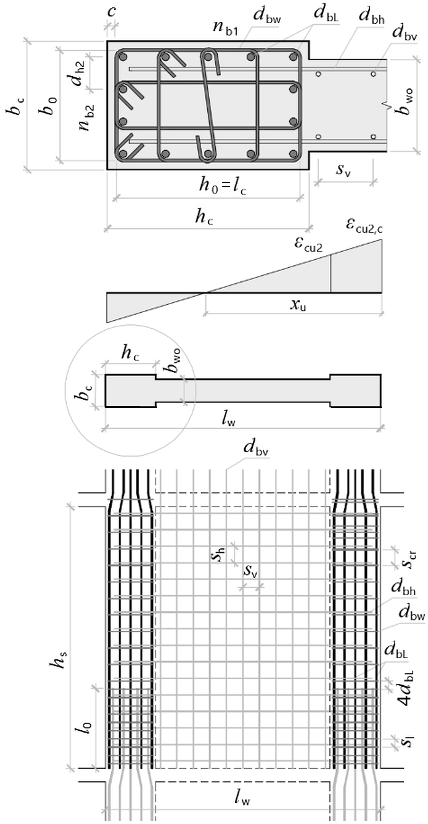
Shear wall dimensions

Length - l_w = 4000  mm

Web thickness - b_wo = 300  mm

Total height - h_w = 19000  mm

Clear storey height - h_s = 3820  mm

Number of storeys - n_s = 6 

Confined zone dimensions

b_c = 300  mm, h_c = 875  mm

Cross section area

Area of confined boundary element

A_f = b_c · h_c = 300 · 875 = 262500 mm²

Web area

A_w =  ( l_w − 2 · h_c )  · b_wo =  ( 4000 − 2 · 875 )  · 300 = 675000 mm²

Total area

A_c = A_w + 2 · A_f = 675000 + 2 · 262500 = 1200000 mm²

Maximum seismic axial load - N_Ed = 2254  kN

 

Concrete   [EN 1992-1-1, Table 3.1]

Characteristic compressive cylinder strength

f_ck = 25  MPa

Partial safety factor - γ_c = 1.5 , α_ct = 1 , α_cc = 1 

Mean value of axial tensile strength

f_ctm = 0.3 · f_ck²³ = 0.3 · 25²³ = 2.564964 MPa

Characteristic axial tensile strength

f_ctk,005 = 0.7 · f_ctm = 0.7 · 2.564964 = 1.795475 MPa

Design compressive cylinder strength

f_cd = α_cc · f_ckγ_c = 1 · 251.5 = 16.666667 MPa

Unconfined concrete ultimate strain

ε_cu2 = 0.0035

Ultimate compressive strain - ε_c2 = 0.002

Longitudinal reinforcement

C = 0 

Characteristic yield strength - f_yk = 500  MPa

Selected steel class B500B

Partial safety factor - γ_s = 1.15

Design yield strength - f_yd = f_ykγ_s = 5001.15 = 434.782609 MPa

Modulus of elasticity - E_s = 200000 MPa

Reinforcement for each confined boundary element

Bar diameter - d_bL = 25  mm

[BS EN 1992-1-1, § 9.5.2 (1)/NA.1]

Minimum bar diameter - d_bL,min = 12 mm

Bar count - n_b = 13 

Bar count along "h₀" - n_b1 = 6 

Bar count along "b₀" - n_b2 = ceiling(n_b2 − n_b1 + 2) = ceiling(132 − 6 + 2) = 3

Reinforcement area

A_s1 = π · d_bL²4 = 3.141593 · 25²4 = 490.873852 mm²

A_s = n_b · A_s1 = 13 · 490.873852 = 6381.360078 mm²

Reinforcement ratio

ρ_L = A_sA_f = 6381.360078262500 = 0.02430994

[§ 5.4.3.4.2 (8)]

Design check: 0.005 ≤ ρ_L = 0.02430994 ≤ 0.04. The check is satisfied! ✓

Vertical web reinforcement

Bar diameter - d_bv = 10  mm

Bar spacing - s_v = 250  mm

[EN 1992-1-1, § 9.6.2 (3)]

Maximum bar spacing

s_v,max = min ( 3 · b_wo; 400 )  = min ( 3 · 300; 400 )  = 400 mm

Single bar area - A_sv1 = π · d_bv²4 = 3.141593 · 10²4 = 78.539816 mm²

Reinforcement ratio - ρ_v = 2 · A_sv1s_v · b_wo = 2 · 78.539816250 · 300 = 0.002094395

[EN 1992-1-1, § 9.6.2 (1)]

Minimum reinforcement ratio - ρ_v,min = 0.002

[§ 5.4.3.4.2 (11)]

Minimum reinforcement ratio for zones with compressive strain > 0.002

ρ_v,min = 0.005

Horizontal web reinforcement

Bar diameter - d_bh = 12  mm

Bar spacing - s_h = 150  mm

[EN 1992-1-1, § 9.6.3 (2)]

Maximum bar spacing - s_h,max = 400 mm

Single bar area - A_sh1 = π · d_bh²4 = 3.141593 · 12²4 = 113.097336 mm²

Reinforcement ratio - ρ_h = 2 · A_sh1s_h · b_wo = 2 · 113.097336150 · 300 = 0.005026548

[EN 1992-1-1, § 9.6.3 (1)]

Minimum reinforcement ratio

ρ_h,min = max ( 0.25 · ρ_v; 0.001 )  = max ( 0.25 · 0.002094395; 0.001 )  = 0.001

 

Transverse reinforcement in confined boundary elements

Characteristic yield strength - f_ywk = 500  MPa

Design yield strength - f_ywd = f_ywkγ_s = 5001.15 = 434.782609 MPa

Concrete cover to hoops - c = 42  mm

Hoop diameter - d_bw = 8  mm

[EN 1992-1-1, § 9.5.3 (1)]

Minimum diameter

d_bw,min = max ( 6; 0.25 · d_bL )  = max ( 6; 0.25 · 25 )  = 6.25 mm

Hoop diameter check:

d_bw = 8 ≥ d_bw,min = 6.25 mm. The check is satisfied! ✓

 

[§ 5.4.3.4.2 (1)]

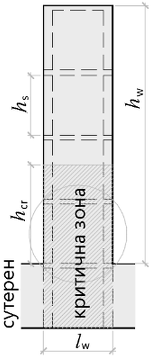
Critical region height

h_{cr_} = max(l_w; h_w6) = max(4000; 190006) = 4000 mm

Must not be greater than

h_cr,max = min ( 2 · l_w; h_s )  = min ( 2 · 4000; 3820 )  = 3820 mm, for number of storeys n_s = 6 ≤ 6

h_cr = min ( h_{cr_}; h_cr,max )  = min ( 4000; 3820 )  = 3820 mm

 

[§ 5.1.2 (1)]

Shear wall dimensions check

l_wb_wo = 4000300 = 13.333333 ≥ 4. The check is satisfied! ✓

[§ 5.4.1.2.3 (1)]

Minimum thickness - b_w,min = max(150; h_s20) = max(150; 382020) = 191 mm

b_wo = 300 mm ≥ b_w,min = 191 mm. The check is satisfied! ✓

[ § 5.4.3.4.2 (6)]

Confined boundary element length

l_c = h_c −  ( d_bw + 2 · c )  = 875 −  ( 8 + 2 · 42 )  = 783 mm

Minimum confined boundary element length

l_c,min = max ( 0.15 · l_w; 1.5 · b_c )  = max ( 0.15 · 4000; 1.5 · 300 )  = 600 mm

l_c = 783 mm ≥ l_c,min = 600 mm. The check is satisfied! ✓

[§ 5.4.3.4.2 (10)]

Minimum confined boundary element thickness

For l_c = 783 mm ≤ max ( 2 · b_c; 0.2 · l_w )  = max ( 2 · 300; 0.2 · 4000 )  = 800 mm:

b_c,min = max(h_s15; 200) = max(382015; 200) = 254.666667 mm

b_c = 300 mm ≥ b_c,min = 254.666667 mm. The check is satisfied! ✓

 

[§ 5.4.3.4.1 (2)]

Check for normalized axial load

ν_d = N_EdA_c · f_cd · 10³ = 22541200000 · 16.666667 · 10³ = 0.1127

ν_d = 0.1127 ≤ 0.4. The check is satisfied! ✓

 

Design anchorage length

η₁ = 1 - when good conditions are provided

η₂ = 1 - for d_bL = 25 ≤ 32 mm

f_ctd = α_ct · f_ctk,005γ_c = 1 · 1.7954751.5 = 1.196983 MPa

[EN 1992-1-1, § 8.4.2 (2)]

f_bd = 2.25 · η₁ · η₂ · f_ctd = 2.25 · 1 · 1 · 1.196983 = 2.693212 MPa

σ_sd = f_yd = 434.782609 MPa

[EN 1992-1-1, § 8.4.3 (2)]

l_b,rqd = d_bL4 · σ_sdf_bd = 254 · 434.7826092.693212 = 1008.977825 mm

[EN 1992-1-1, Table 8.2]

α₁ = 1 , α₂ = 1 , α₃ = 1 , α₅ = 1 , α₆ = 1.5

[EN 1992-1-1, § 8.7.3 (1)]

l_{0_} = α₁ · α₂ · α₃ · α₅ · α₆ · l_b,rqd = 1 · 1 · 1 · 1 · 1.5 · 1008.977825 = 1513.466738 mm

l_0,min = max ( 0.3 · α₆ · l_b,rqd; 15 · d_bL; 200 )  = max ( 0.3 · 1.5 · 1008.977825; 15 · 25; 200 )  = 454.040021 mm

l₀ = round ( max ( l_{0_}; l_0,min )  )  = round ( max ( 1513.466738; 454.040021 )  )  = 1513 mm

 

Confined core dimensions (between centerlines of hoops)

b₀ = b_c −  ( d_bw + 2 · c )  = 300 −  ( 8 + 2 · 42 )  = 208 mm

h₀ = h_c −  ( d_bw + 2 · c )  = 875 −  ( 8 + 2 · 42 )  = 783 mm

Maximum bar spacing

d_b1 = h_c − 2 ·  ( d_bw + c )  − d_bLn_b1 − 1 = 875 − 2 ·  ( 8 + 42 )  − 256 − 1 = 150 mm

d_b2 = b_c − 2 ·  ( d_bw + c )  − d_bLn_b2 − 1 = 300 − 2 ·  ( 8 + 42 )  − 253 − 1 = 87.5 mm

Maximum distance between consecutive longitudinal bars engaged by hoops

[§ 5.4.3.4.2 (9)]

d_h,max = 200 mm

Distance between bars engaged by hoops

n_h1 = max(floor(d_h,maxd_b1); 1) = max(floor(200150); 1) = 1

n_h2 = max(floor(d_h,maxd_b2); 1) = max(floor(20087.5); 1) = 2

Distance between bars engaged by hoops

d_h1 = n_h1 · d_b1 = 1 · 150 = 150

d_h2 = n_h2 · d_b2 = 2 · 87.5 = 175

Distance between bars engaged by hoops

n_h1 = round( ( n_b1 − 1 )  · d_b1d_h1) = round( ( 6 − 1 )  · 150150) = 5

n_h2 = round( ( n_b2 − 1 )  · d_b2d_h2) = round( ( 3 − 1 )  · 87.5175) = 1

 

Hoop spacing in the critical region

[§ 5.4.3.4.2 (9)]

s_cr = min(b₀2; 8 · d_bL; 175) = min(2082; 8 · 25; 175) = 104 mm

Hoop spacing in lap zone

[§ 5.6.3 (3), c)]

s_l = min(100; b_c4) = min(100; 3004) = 75 mm

Hoop spacing outside lap zone

[EN 1992-1-1, § 9.5.3 (3)]

s = min ( b_c; 20 · d_bL; 400 )  = min ( 300; 20 · 25; 400 )  = 300 mm

 

Transverse reinforcement in the lap zone

Required area of one leg

[§ 5.6.3 (4)]

A_st = s_l · d_bL50 · f_ydf_ywd = 75 · 2550 · 434.782609434.782609 = 37.5 mm²

Provided area of one leg

A_sw1 = π · d_bw²4 = 3.141593 · 8²4 = 50.265482 mm²

Design check: A_sw1 = 50.265482 mm² ≥ A_st = 37.5 mm². The check is satisfied! ✓

Check for bar diameters > 20 mm:

Number of legs in the outer 1/3 of lap zone

n_w = round(2 · l₀3 · s_l) = round(2 · 15133 · 75) = 13

Total area of legs in the outer 1/3 of lap zone

ΣA_sw = A_sw1 · n_w = 50.265482 · 13 = 653.451272

[EN 1992-1-1 § 8.7.4.1 (3)]

Design check: ΣA_sw = 653.451272 mm² ≥ A_s1 = 490.873852 mm²

An additional hoop is required for compressed bars

[EN 1992-1-1 § 8.7.4.2 (1)]

at 4 · d_bL = 4 · 25 = 100 mm from the end of the lap zone.

 

Detailing for local ductility in the critical region

Total length of confining links

Σl_i =  ( n_h1 + 1 )  · b₀ +  ( n_h2 + 1 )  · h₀ =  ( 5 + 1 )  · 208 +  ( 1 + 1 )  · 783 = 2814

Mechanical volumetric ratio of confining hoops within the critical region

ω_d = A_sw1 · Σl_ib₀ · h₀ · s_cr · f_ywdf_cd = 50.265482 · 2814208 · 783 · 104 · 434.78260916.666667 = 0.2178507

[§ 5.4.3.2.2 (8)]

The minimum value is 0.08.

Design check: ω_d = 0.2178507 ≥ 0.08 = 0.08 . The check is satisfied! ✓

Sum of the squares of the distances between consecutive engaged bars

Σb2_i = 2 ·  ( n_h1 · d_h1² + n_h2 · d_h2² )  = 2 ·  ( 5 · 150² + 1 · 175² )  = 286250

Confinement effectiveness factors for bars and links

α_n = 1 − Σb2_i6 · b₀ · h₀ = 1 − 2862506 · 208 · 783 = 0.7070664

α_s = (1 − s_cr2 · b₀) · (1 − s_cr2 · h₀) = (1 − 1042 · 208) · (1 − 1042 · 783) = 0.7001916

α = α_n · α_s = 0.7070664 · 0.7001916 = 0.495082

Analysis results

Fundamental period of first vibration mode - T₁ = 0.6795  s

Upper limit period of constant spectral acceleration - T_C = 0.4  s

Basic behavior factor value - q₀ = 3 

Design bending moment - M_Ed = 9591  kNm

Bending moment capacity - M_Rd = 13268  kNm

(The above values refer to the section above the base)

Curvature ductility factor

[§ 5.2.3.4 (3)]

μ_Φ = 2 · q₀ · M_EdM_Rd − 1 = 2 · 3 · 959113268 − 1 = 3.337202 - for T₁ ≥ T_C

[§ 5.2.3.4 (4)]

For steel class B, ductility factor is increased by 50% - μ_Φ = 5.005803

Design value of steel yield strain - ε_sy,d = f_ydE_s = 434.782609200000 = 0.002173913

Mechanical ratio of vertical web reinforcement

ω_v = ρ_v · f_ydf_cd = 0.002094395 · 434.78260916.666667 = 0.05463639

[§ 5.4.3.4.2 (4)]

Design check: αω_d ≥ αω_{d_min} = 30·μ_Φ·(ν_d + ω_v )·ε_{sy_d}·b_c/b₀ – 0.035

αω_d = α · ω_d = 0.495082 · 0.2178507 = 0.1078539

αω_d,min = 30 · μ_Φ ·  ( ν_d + ω_v )  · ε_sy,d · b_cb₀ − 0.035 = 30 · 5.005803 ·  ( 0.1127 + 0.05463639 )  · 0.002173913 · 300208 − 0.035 = 0.04379262

The required curvature ductility is provided: αω_d = 0.1078539 ≥ αω_d,min = 0.04379262 . ✓

Ultimate strain of confined concrete

ε_cu2,c = 0.0035 + 0.1 · αω_d = 0.0035 + 0.1 · 0.1078539 = 0.01428539

Neutral axis depth at ultimate curvature

x_u =  ( ν_d + ω_v )  · l_w · b_cb₀ =  ( 0.1127 + 0.05463639 )  · 4000 · 300208 = 965.402273 mm

Confined boundary element length

l_c,req = x_u · (1 − ε_cu2ε_cu2,c) = 965.402273 · (1 − 0.00350.01428539) = 728.873416 mm

Design check: l_c = 783 mm ≥ l_c,req = 728.873416 mm. The check is satisfied! ✓

NOTE: All references are according to EN 1998-1, unless noted otherwise.